Tónová mřížka

Tónovou mřížku jsem objevil někdy kolem roku 1995. Jak se později ukázalo, vskutku nejsem jejím objevitelem. (V lednu 2009 jsem se dozvěděl, že mřížku vynalezl Leonhard Euler. Pan Euler byl prostě moc aktivní a vyžral všechnu zajímavou matiku na staletí dopředu. Kdybyste mřížku chtěli hledat v cizojazyčné literatuře, hledejte německý výraz Tonnetz, případně Euler Tonnetz.) Původně mi mřížka sloužila hlavně pro rychlé odvozování akordů, což zůstalo i jejím hlavním účelem. 

Mřížka vypadá na první pohled jako chaotický shluk tónů. Ale jsou v ní určité zákonitosti. Mimochodem je nekonečná, ale tóny se v ní pravidelně opakují. Toto je její výřez. 

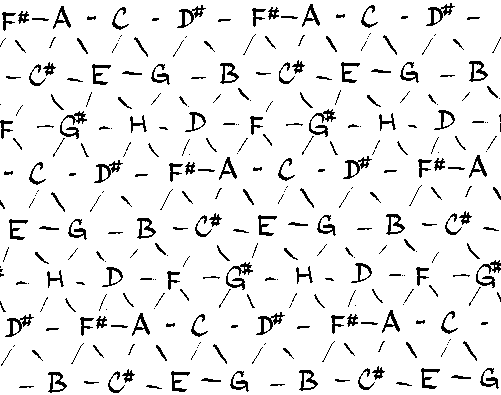
Hledání akordů

Každý trojúhelník je normální akord. Durové špičkou nahoru, mollové špičkou dolů. Jeden tón z trojúhelníku akord pojemenovává.

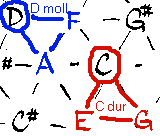
Každý druh akordu má svojí "masku", která když se přiloží na mřížku, tak se dá přečíst složení akordu.

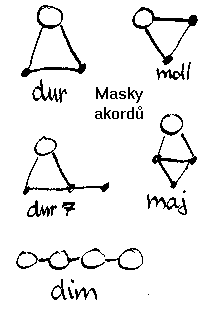
Každá maska obsahuje alespoň jeden kroužek, který označuje základní tón (tón, podle kterého se akord jmenuje).

Např. když vezmu masku akordu Maj a přiložím kroužek na tón F, tak přečtu složení akordu F Maj: F C A E.

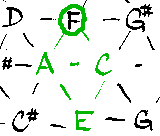
Akord Dim má zvláštní složení, protože každý jeho tón jej zároveň pojmenovává. Tak například A dim je totéž, co C dim.

Takže s pomocí tónové mřížky můžete určit složení všech akordů.

Složitější akordy

Když se podíváte na trojúhelník základního akordu, můžete si všimnout, že má ze všech stran přesně devět sousedů. Takže si můžete udělat masku na libovolný složitější akord (devítky, maje, jedenáctky apod.), která bude mít tvar trojúhelníka s nejčastěji jedním ocáskem.

Mám tón, hledám akord

V praxi jsem se často dostal do situace, kdy jsem do písně hledal akord a prostě jsem nevěděl. Přitom je vždycky z akordu slyšet alespoň jeden tón (většinou poslední tón taktu). Tónová mřížka mi názorně ukazuje, které akordy by se tam mohly hodit -- jsou to trojúhelníky kolem známého tónu.

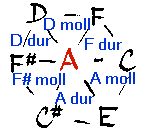
Dejme tomu, že vím, že ve hledaném akordu je tón A. Potom mám na výběr jenom šest normálních akordů (a pár nenormálních), což se dá rychle vyzkoušet.

Nějaké další postřehy kolem odvozování akordů.

Hledám souzvuk

Dva sousední tóny v mřížce tvoří ladný souzvuk. Tóny, které spolu nesousedí, znějí dohromady disharmonicky. 

Další využití

Na tónové mřížce se kromě akordů dají hledat stupnice, kadence, pentatoniky a spousta dalších maličkostí. Zatím mě to nebaví vypisovat, ale věřím, že si to tam všechno najdete, budete-li chtít. Například grafické znázornění normálních akordů tóniny C dur, tedy kadence C dur:

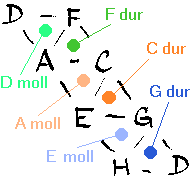
Zároveň je tímto obrázkem naznačeno, jak se najde v mřížce normální stupnice.

Jak zkonstruovat mřížku

Nejlepší je mřížku si vytisknout, ale když ji potřebujete nakreslit, tak je dobré vědět, jak na to. (Já si ji třeba vždycky znovu kreslím, protože papíry ztrácím).

V severozápadním směru je to normální kvartový kruh, to jest postupuje se po pěti (sedmi) půltónech. Ve vodorovném směru se postupuje po třech půltónech a v severovýchodním po čtyřech. Pokud chcete přijít na kloub tomu, proč je to zrovna 3, 4 a 5, tak protože to jsou ladné souzvuky (případně mrkněte na matematické vysvětlení).

Další: Odvození akordů